격자 게이지 이론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
격자 게이지 이론은 시공간을 격자 구조로 이산화하여 게이지 이론을 구성하는 방법이다. 이 이론은 페르미온을 격자점에, 게이지장을 링크에 배치하며, 몬테카를로 방법 등을 사용하여 입자 질량과 같은 물리량을 계산한다. 격자 게이지 이론은 양자 자명성 연구에 중요하며, 힉스 보손 질량 예측 등에 활용될 수 있다. 또한, 상전이 현상 연구 및 스핀 거품 모델과 관련이 있다.
더 읽어볼만한 페이지
- 격자장론 - 윌슨 고리
윌슨 고리는 게이지 이론에서 폐곡선을 따라 게이지 퍼텐셜을 경로 순서화하여 지수화한 값의 대각합으로 정의되는 게이지 불변량이며, 쿼크 가둠 현상 설명, 쿼크-반쿼크 쌍 사이의 포텐셜 계산, 가둠 상전이 구별 등에 활용된다.
2. 이론의 기초
격자 게이지 이론은 양자장론과 달리 민코프스키 공간에서 윅 회전을 통해 유클리드 공간으로 옮겨 시간과 공간을 동등하게 다룬다. 이산화된 시공간인 "격자" 위에서 장론을 구성하는데, 페르미온은 격자점(사이트)에, 게이지장은 인접한 사이트를 연결하는 선(링크) 위에 놓인다. 게이지장은 시공간의 방향을 가진 벡터장으로 표현되며, '''링크 변수'''라고 불린다.
콤팩트 군 리 군 ''G''(리 대수가 아님)의 원소 ''U''가 각 링크에 할당된다. 예를 들어, SU(3)으로 양자색역학(QCD)를 시뮬레이션하기 위해 각 링크에 3×3 유니타리 행렬이 정의된다. 링크에는 방향이 있으며, 역원은 반대 방향의 동일한 링크에 해당한다. 각 노드에는 (색상 3-벡터, SU(3)의 기본 표현이 작용하는 공간), 비스피너(디랙 4-스피너), ''nf'' 벡터 및 그래스만 수 변수 값이 주어진다.
경로를 따른 링크의 SU(3) 원소 구성(행렬의 순서화된 곱셈)은 경로 정렬 지수(기하학적 적분)에 가깝고, 닫힌 경로에 대해 윌슨 루프 값을 계산할 수 있다.
2. 1. 페르미온 더블링
디랙장의 작용을 가장 단순한 형식으로 이산화하면 여분의 자유도가 나타나는 페르미온 더블링 문제가 발생한다. 이 문제를 피하기 위해, 실제 계산에서는 몇 가지 종류의 개량된 작용이 사용되고 있다.3. 양-밀스 작용
양-밀스 작용은 윌슨 고리(케네스 G. 윌슨이 제안)를 사용하여 격자 위에 표현되며, 격자 간격 가 0으로 수렴할 때 원래의 연속체 작용을 형식적으로 재현한다.[13] ''G''의 충실한 기약표현 ρ가 주어지면, 윌슨 작용으로 알려진 격자 양-밀스 작용은 윌슨 고리 안의 ''n'' 링크들 ''e'' 1, ...,''e''n에 대한 대각합(의 실수 성분)의 모든 격자 사이트에 대한 합으로 주어진다.
:
여기서 χ는 특성이다. ρ가 실수 (또는 유사실수) 표현인 경우, 윌슨 고리의 방향이 반전되더라도 작용에 대한 기여도는 변경되지 않기 때문에 실수 성분을 취하는 것은 중복된다.
작용에 사용되는 윌슨 고리에 따라 다양한 윌슨 작용이 가능하다. 가장 간단한 윌슨 작용은 1×1 윌슨 고리만 사용하며 작은 격자 간격 에 비례하는 "격자 인공물"이 연속체 작용과 다르다. "향상된 작용"을 구성하기 위해 더 복잡한 윌슨 고리를 사용함으로써 격자 아티팩트는 에 비례하도록 줄일 수 있으며, 이는 계산이 더 정확해짐을 의미한다.[1]
4. 측정 및 계산
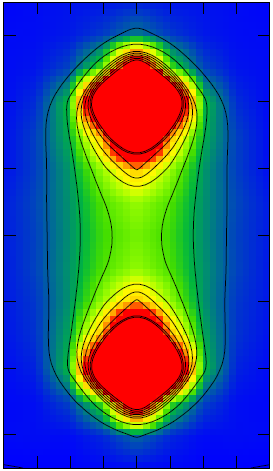
입자 질량과 같은 물리량은 몬테카를로 방법 등의 기술을 사용하여 확률론적으로 계산된다. 게이지장 배치는 에 비례하는 확률로 생성되는데, 여기서 는 격자 작용이고 는 격자 간격 와 관련이 있다. 관심 있는 물리량은 각 배치에 대해 계산되고 평균화된다. 일 때 결과를 연속체로 외삽할 수 있도록 계산은 종종 서로 다른 격자 간격 에서 반복된다.
4. 1. 격자 QCD 계산
격자 양자색역학(QCD) 계산 결과는 중간자에서 입자(쿼크 및 반쿼크)뿐만 아니라 글루온 장의 "자속관"도 중요하다는 것을 보여준다.[14]입자 질량과 같은 양은 몬테카를로 방법과 같은 기술을 사용하여 확률론적으로 계산된다. 게이지 장 구성은 에 비례하는 확률로 생성되는데, 여기서 는 격자 작용이고 는 격자 간격 와 관련이 있다. 관심 수량은 각 구성에 대해 계산되어 평균화된다. 일 때 결과를 연속체로 외삽할 수 있도록 계산은 종종 서로 다른 격자 간격 에서 반복된다.
이러한 계산은 종종 극도로 계산 집약적이며 사용 가능한 가장 큰 슈퍼컴퓨터를 사용해야 할 수도 있다. 계산 부담을 줄이기 위해 페르미온 장을 비동적 "동결" 변수로 처리하는 소위 담금질 근사법을 사용할 수 있다. 이는 초기 격자 양자색역학 계산에서는 일반적이었지만, 이제는 "동역학적" 페르미온이 표준이다.[15] 이러한 시뮬레이션은 일반적으로 분자 역학 또는 미시정규 앙상블 알고리즘을 기반으로 하는 알고리즘을 활용한다.[16][17]
4. 2. 전산 자원
이러한 계산은 매우 많은 전산 자원을 필요로 하며, 사용 가능한 가장 큰 슈퍼컴퓨터를 활용해야 할 수도 있다. 계산 부담을 줄이기 위해 페르미온 장을 비동역학적 "동결" 변수로 처리하는 소위 담금질 근사법을 사용할 수 있다. 이는 초기 격자 양자색역학 계산에서는 일반적이었지만, 현재는 "동역학적" 페르미온을 사용하는 것이 표준이다.[15] 이러한 시뮬레이션은 일반적으로 분자 역학 또는 미시정규 앙상블 알고리즘을 기반으로 하는 알고리즘을 활용한다.[16][17]5. 양자적 자명함
격자 게이지 이론은 실수 공간 재규격화군을 통한 양자 자명성 연구에도 중요하다.[18] 재규격화군 흐름에서 가장 중요한 정보는 ''고정점''이라고 불리는 것이다.
대규모로 시스템의 가능한 거시적 상태는 이 고정점 세트에 의해 제공된다. 이러한 고정점이 자유장론에 해당하는 경우 해당 이론은 ''자명''하거나 상호작용하지 않는다고 한다. 격자 힉스 이론 연구에는 수많은 고정점이 나타나지만, 이들과 관련된 양자장론의 본질은 여전히 미해결 문제로 남아 있다.[19]
자명함은 아직 엄격하게 입증되지 않았지만 격자 계산은 이에 대한 강력한 증거를 제공했다. 이 사실은 양자의 자명함을 사용하여 힉스 보손의 질량과 같은 매개변수를 제한하거나 예측할 수 있기 때문에 중요하다.[8]
6. 기타 응용
1971년 프란츠 베그너는 상전이 현상을 연구하면서 흥미로운 통계적 특성을 갖는 2차원 격자 게이지 이론 모델을 제시하였다.[20] 1x1 윌슨 고리만 작용에 나타나는 격자 게이지 이론은 스핀 거품 모델과 쌍대 관계를 갖는다.[21][10]
참조
[1]
논문
Confinement of quarks
[2]
논문
Lattice QCD computation of the color fields for the static hybrid quark-gluon-antiquark system, and microscopic study of the Casimir scaling
2010-02-03
[3]
논문
Nonperturbative QCD simulations with 2+1 flavors of improved staggered quarks
[4]
논문
Microcanonical Ensemble Formulation of Lattice Gauge Theory
[5]
논문
Lattice gauge theory in the microcanonical ensemble
https://cds.cern.ch/[...]
[6]
논문
The renormalization group: Critical phenomena and the Kondo problem
American Physical Society (APS)
1975-10-01
[7]
논문
Triviality Pursuit: Can Elementary Scalar Particles Exist?
[8]
논문
Is the standard model Higgs mass predictable?
https://cds.cern.ch/[...]
[9]
간행물
Duality in Generalized Ising Models and Phase Transitions without Local Order Parameter
http://www.tphys.uni[...]
[10]
논문
The dual of pure non-Abelian lattice gauge theory as a spin foam model
[11]
논문
Confinement of quarks
[12]
논문
Monte Carlo study of quantized SU(2) gauge theory
[13]
논문
Confinement of quarks
[14]
논문
Lattice QCD computation of the color fields for the static hybrid quark-gluon-antiquark system, and microscopic study of the Casimir scaling
[15]
논문
Nonperturbative QCD simulations with 2+1 flavors of improved staggered quarks
[16]
논문
Microcanonical Ensemble Formulation of Lattice Gauge Theory
[17]
논문
Lattice gauge theory in the microcanonical ensemble
https://cds.cern.ch/[...]
[18]
논문
The renormalization group: Critical phenomena and the Kondo problem
[19]
논문
Triviality Pursuit: Can Elementary Scalar Particles Exist?
[20]
간행물
Duality in Generalized Ising Models and Phase Transitions without Local Order Parameter
http://www.tphys.uni[...]
[21]
논문
The dual of pure non-Abelian lattice gauge theory as a spin foam model
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

